How to reduce the noise in the high gain models

In this guide, we will show how to diagnose and reduce the unwanted noise (buzz or hum) of high gain models.

Why high gain models can produce unwanted noise?

Like the real amplifiers, also the digital emulation may suffer from unwanted noise on the high gain models. This happens because the amplifier needs to apply a lot of gain to the input signal in order to produce the distortion: some models may amplify the input by more than 2-3000 times.
Everything at the input is amplified: the guitar tone and the noise as well.
The larger the gain, the louder will be the output noise.

IMPORTANT!
The digital amp models does not generate noise by themselves. They simply amplify the noise at the input.

How to reduce the unwanted noise

In order to reduce the unwanted noise, there are three things you can do:

1. lower the gain of the amp model
2. reduce the sources of noise
3. use noise suppressors

Point 1 changes the amp response and it is not always possible if you need that high gain tone. So let see more in details the Point 2

How to reduce the sources of noise

1. Some pickups are noisier than others. Especially the single coil pickups can collect a lot of environmental electrical noise. If possible, use humbucker pickups which are much less sensitive to noise.
2. Make sure whether the grounding of the guitar is properly done.
3. Try to move in the room with your guitar to find a better position. You should move away from the electromagnetic sources like power suppliers, ac adaptors, neon lamps, computer screens. Sometimes it is enough to change orientation of the guitar by turning 90 degrees.
4. Make sure to use a good shielded guitar cable, and prefer a shorter one

With digital devices the noise can be generated by the audio interface, especially the ones which are USB powered. Many computer have a noisy USB power supply, and that noise reaches the audio interface inputs. To fix this:

5. Try to connect the computer and audio interface AC adaptors to a different power socket
6. If you are using a laptop or a tablet, disconnect them from the power supplier and use the battery
7. Plug the audio interface to a different usb port
8. Avoid cheaper audio interfaces which usually do not have good filters on the power supply.

Noise suppressors

These are the last resort because they may alter the dynamic of the guitar tone.
Noise suppressors should be used at the very beginning of the sound chain and definitely before any distortion pedal or amplifier to let them work more efficiently.
There is not a universal setting for an Expander Gate pedal: it depends on how much the setup is noisy. For a very noisy setup, you need to use a higher threshold setting. Doing so, however, could produce audible artefacts.
That’s why in Overloud we prefer not to add the noise suppressor pedals into the factory preset. Because each of them would need individual settings depending on the current setup.

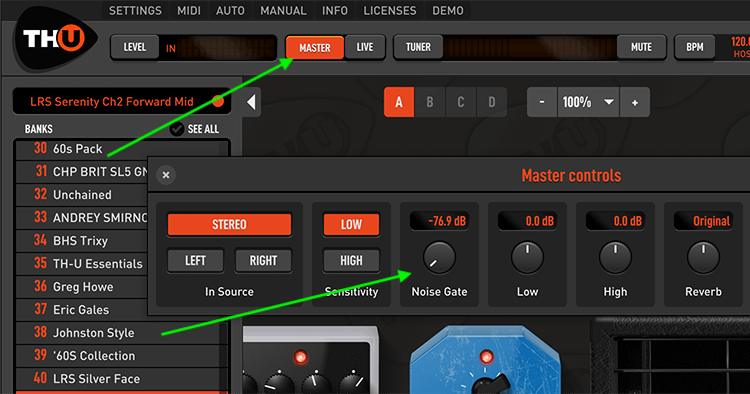
Instead, we recommend to use the TH-U Noise Gate from TH-U Master section. You set it once for your setup and the noise gate is applied to all presets. In any case you can still use the Noise Gate pedal with specific presets needing additional adjustment.